-------

Hoe Ornithopters Vliegen

Flagge flag vlag pavillon

Het Handboek

Inhoud:

1. Handboek

(handboek Wie Ornithopter fliegen in het Duits)

Titelblad van het handboek

Hoe wekt een ornithopter, ondanks de wisselende slagrichting, trekkracht en liftkracht? In het handboek wordt het antwoord, gebaseerd op bekende onderzoeksresultaten, geleverd.

Naast de aerodynamische eigenschappen van de op- en neergaande slag komt ook de dynamiek van de slagvleugel aan de orde. Daartoe worden de benodigde vergelijkingen en een rekenschema aangereikt. Deze bevatten de bepaling van het krachtenevenwicht voor een staionaire vlucht en de voor de modelbouw de zo belangrijke beschrijving van de benodigde vleugelverdraaiïng.

Met een zelf te maken rekenprogramma zijn de uitwerkingen van de verscheidene modelpameters van de prestatiegegevens van een ornithopter te bepalen. Ook optimalisaties zijn op meerdere manieren mogelijk. Met dergelijke getalswaarden is men voor de beoordeling van de slagvlucht niet langer meer afhankelijk van aannames en mondelinge beschrijvingen.

Bovendien zijn in het handboek de uitkomsten van een rekenmodel-voorbeeld weergegeven (overeenkomstig het model EV7). Een hele reeks van variaties van dit rekenemodel zijn in afzonderlijke hoofdstukken uitgelegd en de veranderingen in diagrammen vastgelegd. Ook zonder eigen berekeningen kan men daaruit interessante verbanden binnen de slagvleugeltechniek herkennen en op waarde schatten. Dat alles is met nuttige aanwijzingen uit de ornithopter-modelpraktijk verrijkt.

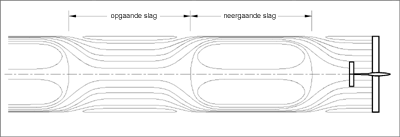
Wervelsysteem langs het traject
Wervelsysteem achter een ornithopter
onder quasi-stationaire stroomcondities

Het ornithopterthema valt ook binnen het vakgebied van de Bionica. Er wordt daarom geprobeerd, door het begrijpen van de verschijningsprincipes van de vleugel, vliegwaardige ornithopters te ontwikkelen.

U kunt het handboek (in het Duits) en de daarbij behorende foto's downloaden.

  • PDF 3.3 MB
  • PDF 5.9 MB
  • PDF 9.2 MB

Het handboek is door Jean-Louis Solignac in het Frans vertaald. Met zijn vakkennis als aerodynamicus en zijn ervaring heeft hij veel aan de verbetering van het handboek bijgedragen. Zijn vertaling vindt U op de Franse pagina.

Jean-Louis Solignac, Maître de Recherche, était Chef de Division Adjoint Aérodynamique Fondamentale de la Direction Aérodynamique de l'O.N.E.R.A. (Office National d'Etudes et de Recherches Aérospatiales).

The photos of the handbook

Titelblad Langsvliegen Vleugel in de bovenste slagpositie Linkerbocht Hellingstart Ornithopter type EV7 Aanvliegen met slagpennen Voortzetting van het aanvliegen Vleugelverdraaiing tijdens de opgaande slag Vleugelverdraaiing tijdens de neergaande slag Vleugelverdraaiing tijdens de glijvlucht Overvliegen Geen ornithopterzwerm Kijkje op het aandrijfmechanisme Inpassingen in de romp
toets

2. Slagvleugelberekeningen
onder aanname van quasi-stationaire omstandigheden

De de vergelijkingen in het handboek worden in verschillende Orni- rekenprogramma's toegepast. daaraan ligt het navolgende rekenprogramma ten grondslag.

Daarbij wordt de slagvleugel in gedachten eerst in stroken met een zeer kleine spanwijdte verdeeld. Dan berekent men voor elk van deze vleugelsecties de aërodynamische krachten onder stationaire c.q. constante aanstroomvoorwaarden. Het optellen van al deze krachtjes levert de totale aërodynamische kracht op voor de hele spanwijdte.

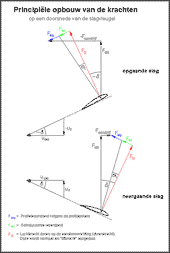
Krachten op een doorsnede van de slagvleugel
Opbouw van de krachten

Op die manier krijgt men de totale lift- en trekkracht van de slagvleugel ten aanzien van en bepaald tijdstip tijdens de slagperiode. Ook is de daarbij behorende vleugelverdraaiing, de profiel- en geïnduceerde weerstand gedurende de loop van dit rekenschema te bepalen.

Reken ondersteunende filters
Rekenverdelingen

Deze handeling wordt met gelijkmatige tussenpozen van de vleugel­slagbeweging herhaald. Daarbij baseert men zich meestal op de veranderde waarden zoals bijvoorbeeld de circulatieverdeling, de aanstromingsverhoudingen en de V-stelling van de vleugel. Gelijktijdig gaat met uit van stationaire omstandigheden. Er wordt hierbij aangenomen dat de stroming zich binnen de tijdstap van de berekening niet veranderd. Met niet-stationaire stromingen wordt geen rekening gehouden.

Op deze manier, dus door het aan elkaar rijgen van van de verschillende stationaire toestanden, wordt het temporele verloop van de krachten onder quasi-stationaire voorwaarden bepaald.

De kracht van een gehele slagbeweging krijgt men door het optellen van het krachtverloop over de beschouwde tijdspanne. De op- en neergaande slag van de vleugel wordt afhankelijk van de toepassing afzonderlijk beschouwd. Ten slotte leidt het samennemen van de krachten van de op- en de neergaande slag tot de totaalkrachten gedurende de gehele slagperiode.

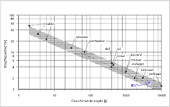
slagfrequentie/gewicht van de vogels
Slagfrequentie en
het gewicht van vogels
van Literatuur Heinrich Hertel

Volgens Literatuur Erich von Holst leidt de quasi-stationaire methode alleen maar bij een hoge voorwaartse snelheid met relatief lage slagfrequenties tot bruikbare resultaten (grote vogels). Anderzijds worden de invloeden door de niet-stationaire aanstroomverhoudingen te groot. Nieuwe onderzoeken bevestigen deze beperking, zoals bijvoorbeeld volgt uit de analyse van M. Neef.

krachten van een slagvleugel
Herziene principe ordening van de krachten op de positie van een slagvleugel

In de Handboek heb ik geprobeerd de fysieke hoeveelheden van een slagvleugel te beschrijven voor een rekenmodel. In Configuratie van de krachten aan de slagvleugel (in het Duits, PDF 0.5 MB) worden enkele daarvan opnieuw gedefinieerd.

toets

3. Onderzoeksresultaat

Dr.-Ing. Matthias F. Neef heeft in zijn dissertatie Analyse des Schlagfluges durch numerische Strömungsberechnung de niet-staionaire stroming rond een bewegende vleugel onderzocht. Daarbij lukte het hem een soortgelijk wervelsysteem, als hierboven afgebeeld, aan te tonen. Zijn afbeelding is echter veelnauwkeuriger en gedetailleerder, maar onder transiënte stroomcondities.

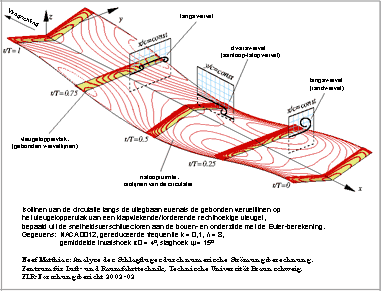
Isolijnen tijdens de slagvlucht
Isolijnen van de circulatie langs een vliegbaan
onder transiënte stroomcondities

De dissertatie bevat een overzicht van een slagvlucht en nog meer zeer interessante afbeeldingen (zie externe link 1en 2).

toets

4. De randwervels van de slagvleugel

De boven afgebeelde isolijnen van de circulatie van een slagvleugel kan men zich ook als losse werveldraden voorstellen.

Naast elkaar liggende werveldraden met dezelfde circulatierichting voegen zich in de afgaande stroming van de vleugel in hun gemeenschappelijke centrum samen tot één enkele wervel.

Randwervels langs het traject
Randwervels van de slagvleugel

Op deze manier groeit het grootste deel van de werveldraden aan één vleugelzijde aan tot een gemeenschappelijke randwervel. Zijn aangrijpingspunt aan de achterzijde van de slagvleugel beweegt zich gedurende een slagperiode heen en weer, in het bijzonder tijdens de opgaande slag. De achter de slagvleugel hangende wervelband toont dus in het bovenaanzicht in regelmatige afstanden zijdelingse insnoeringen.

Ook bij vogels wordt de zijdelingse beweging van het aangrijpngspunt van de wervelaangrijpingspunten aan de achterkant van de vleugels al vastgesteld (zie externe link 3, Fig. 1). De daarbij gekozen beschrijving van de vluchtwijze kan men door continue wervelverloop vertalen (zie de beschrijving van de verschillende Bewegingsovergang bij vogels).

Vleugelrandwervels van een vogel
Spiraalvormige vleugel­randwervelingen resp. stuwstraal van een vogel in de continue wervelbeweging tijdens de kruisvlucht of in distancevlucht

Wanneer men zich de randwervels in de hiernaast staande afbeelding ruimtelijk voorstelt, dan ontstaat er een verrassend beeld.

Het wervel­aangrijpngspunt van een vleugelkant verloopt gedurend een slagperiode niet alleen aan de achterzijde van de vleugel heen en weer. Ze volgt ook de slagbeweging. Beide bewegingen tezamen veroorzaken, in de vluchtring gezien, een ietwat ringvormige baan. Betrekt men nu ook nog de voorwaarts gerichte beweging van de slagvleuegls hierin, dan herkent men de schroefvormige beeld van de beide naar achteren ontstane vleugelrandwervels.

Ook de randwervels van een propeller zijn schroefvormig opgebouwd (zie externe link 4). Ze omhullen de aandrijfstraal en zijn een wezenlijk bestanddeel ervan.in tegenstelling tot de propeller zijn bij de slagvleugels de windingen van de randwervels echter uit elkaar getrokken. In het 3-dimensionale aanzicht van dit wervelbeeld herkent men daarom aan iedere vleugelkant een aandrijfstraal.

Een met dit principe overeenkomstig wervelbeeld moet ook bij ornithopters tijdens de trekvluvht worden nagestreeft. For more information, please see the article Arrangements of wing tip vortices on flapping wings, versie 4.2, (PDF 0.5 MB).

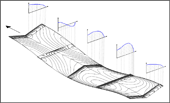
Lift-verdelingen volgens het vortexbeeld
Reconstructie van de
lift-verdelingen

Uit een dergelijk vortexbeeld kan men de liftverdelingen aan de vleugel afleiden. De positie van de vortexdraden aan de achterste rand van de slagvleugel wordt hiervoor gebruikt. Elke vortexdraad komt overeen met een fase van dezelfde liftgrootte. Voor meer informatie over de procedure, zie Arrangements of wing tip vortices on flapping wings, versie 4.2, (PDF 0.5 MB).

Opvallend is dat de liftverdeling in de onderste slagpositie aanzienlijk groter is dan in de bovenste slagpositie. This is due to the aerodynamic phase shift under non-steady flow conditions. In this way, the large lift of the downstroke remains effective even in the lower final stroke position. The same applies to the upper final stroke position, where the lift is influenced by the small lift distribution of the previous upstroke (zie Dissertatie van Dr.-Ing. Matthias F. Neef, bijv. pagina 204, afbeelding 99, externe link 1).

Vortex-ringen in het slagvlucht
Vortex-ringen langs de vliegbaan in het slagvlucht

Lift components that are not shifted, but will be built up and down with each wing beat, leaves vortex rings along the flight path. They occur in addition to the wing tip vortices. Especially the starting vortices of the vortex rings increase the induced drag. This is also true for negative lift. In the shown example, the vortex-rings are arranged phase-shifted to the flapping motion.

At upstroke, the source of the vortex rings is clear. Negative lift exists in the hand wing area. It cannot be taken over from the arm wing. Therefore, it has to be generated again on both wing sides with every wing beat. This produces the two vortex rings.

During the downstroke, in principle, the hand wing can take positive lift from the arm wing. In the present case, however, this is not enough for the downstroke (please see above image). Therefore, a part of the lift has to be built up and taken down again with every wing beat. Thereby in particular a large vortex ring is formed here, which encloses the arm and hand wings of both wing sides together. It consists of relatively large numbers of vortex filaments here and is correspondingly strong, stronger than the wing tip vortex. This corresponds in a first approximation to a Ring-vortex gait.

In addition, a small vortex ring is created on each wing side in the hand wing area. It results from the increased lift in this area. Therefore, it is more advantageous to work with ongeveer constante lift during a flapping period.

comparison of the induced drags
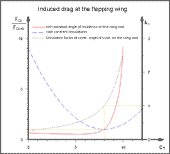
Induced drag
- at constant circulation and
- at constant angle of inci­dence at the wing root.
Its size is related to the induced drag of an elliptical lift distribution.

Energy is required for the formation of the wing tip vortices. The size of the associated losses can be described with the help of the induced drag (F_di). In the design of Distance and cruising flights it is good to know the tendency of the induced drag. It is determined here using the calculation method by reference R. T. Jones (1950). For its delineation the induced drag of the elliptical lift distribution (F_di ell) serves as reference value. As is well known, the induced drag has thereby its minimum in wings with limited wingspan. If the circulation-characteristic-number c_Γ (c-gamma) is varied, this results in the adjacent diagram (as in the handbook, Fig. 3.2).

The circulation factor k_Γ (k-Gamma) also shown is also related to a wing flying with elliptical circulation or lift distribution in gliding flight (k_Γ = 1). The basis is always the model from the handbook.

For a flapping flight with smaller upstroke circulation-characteristic-number than five and with approximately constant lift, therefore, a bending of the hand wing is very useful. Its winglet effect reduces the flow along the wing and thus the induced drag. This increases the efficiency factor of the flapping wing. The point of attachment of the wingtip vertebra to the trailing edge of the wing s lies always close to the wrist during upstroke, regardless of whether the hand wing is bent downward strongly or only slightly (please see also the flight modes distancevlucht an kruisvlucht).

toets

5. De formatievlucht van vogels

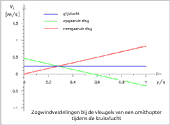
zogwindverdelingen tijdens de slagvlucht
Zogwindverdelingen bij de vleugels van een ornithopter tijdens de kruisvlucht

In V-vormig gerangschikte vliegformaties van vogels treedt bij separate individuen een meetbare vermogens­besparing op. Deze komt in het bijzonder door de aerodynamische invloeden tot stand. Met behulp van de slagvleugeltheorie van een ornithopter kunnen conclusies t.a.v. de manier van energiebesparing worden getrokken.

When a bird joins a flight formation during migration, an energy saving can be observed. Especially waterfowl use the formation flight. However, the energy savings may also be as a result of the transition from distancevlucht to kruisvlucht.

In samenhang met zijn lift veroorzaakt de naar voren vliegende vogel aan zijn beide vleugeltippen automatisch een vleugelrandwervel. Voor hen betekent dit energ ie­verlies. Dit is m.n. voor vogels met een hoge vleugelbelasting en korte spitse vleugelvormen relatief hoog. De achteropkomende vogels kunnen echter proberen, de energie van de beide randwervels voor het verminderen van hun vlieginspanning te benutten.

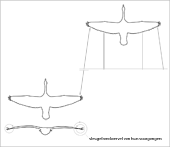
formatievlucht van vogels
Weerstandsafname tijdens de formatievlucht van vogels

Bekend is de hypothese dat de achteropkomende vogel een stijgwindveld van zijn voorganger benut (zie externe link 5). Deze wordt aan de naar achteren gerichte randwervel van de vliegformatie onttrokken. Deze stijgwind maakt het mogelijk voor de achteropkomende vogel zijn eigen vermogen te vergroten, zonder zelf toegevoegde arbeid te verrichten. Het is voor hen echter efficiënter de draai-impuls van de aankomende randwervel te gebruiken om zijn eigen randwervel te veroorzaken (zie de hiernaaststaande afbeelding en externe link 6).

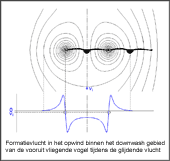
formatievlucht in het downwash gebied
Formatievlucht met opwind binnen het downwash gebied van de vooruit vliegende vogel tijdens de glijdende vlucht
Daaronder wordt het verloop van de snelheid van het downwash gebied achter de voorliggende vogel getoond, gebaseerd op het omliggende luchtruim.
Tijdens de slagvlucht beweegt de vleugelrandwervels permanent langs de achterkant van de slagvleugel heen en weer.

The benefits of this one-sided up wind is questionable already in gliding flight. This is especially true in flapping flight, because with it the distance between the two wing tip vortices changes cyclically (please see the article Arrangements of wing tip vortices on flapping wings, versie 4.2, (PDF 0.5 MB). However, it seems possible, at least in gliding flight, to use the torque of the tip vortex of the bird flying ahead to reduce the rotation of the own counter-rotating wing tip vortex (please see related link 6). But gliding birds in formation flight you only see very rarely in nature and surely also only for a short time (please see related link 7).

arrangement of birds and their tip vortices
This is the most probable arrangement of birds and their wing tip vortices during flight in V-formation

In the paper some theses of formation flight are described and how its benefit might be achieved. The most probable configuration of the bird arrangement is shown here on the right. Similar to two counter-rotating propellers arranged one behind the other, the trailing bird works with a higher efficiency. However, part of the drop in performance when joining the V-formation may also result in a final transition from distance flight to cruise flight.

Formatievlucht van vogels, van Titus Tscharntke
Formatievlucht van vogels
Fotograaf Titus Tscharntke

Het probleem van de achterop komende vogel is de optimale instelling van alle afstanden in de driedimensionale ruimte achter de voor hun vliegende vogel. Deze moet proberen de afstanden t.o.v. de klapwiekende vleugel van zijn voorganger zo aan te passen dat het juiste werveldeel van de voorganger op het juiste moment en op de optimale plaats hem treft. Hij kan de beste vliegpositie zeker voelen maar moet daarbij echter toch ook compromissen sluiten. In de theorie van de formatievlucht van vogels zijn er nog veel onbeantwoorde vragen. Meer daarover in het Handboek, bijlage E (zie download opstijgen) and the article Arrangements of wing tip vortices on flapping wings, versie 4.2, (PDF 0.5 MB).