Handbuch
Traduction en français de Jean-Louis Solignac
1. Handbuch

Comment un ornithoptère produit - il poussée et portance - en changeant alternativement la direction du battement? La réponse en est donnée dans le handbuch sur la base de résultats connus de la recherche. A côté des propriétés aérodynamiques des battements en élévation et en abattée, la dynamique de l'aile est aussi prise en considération. Les relations sont exposées à l'aide d'équations et de diagrammes. On peut ainsi faire quelques calculs et réaliser une aile battante à son idée. Le tout est enrichi d'avertissements utiles provenant de la pratique du vol de maquettes d'ornithoptères.
Les équations relativement simples exposées pour changer la répartition de la circulation permettent de faire varier la portance et de trouver la torsion adéquate à donner à l'aile.
-
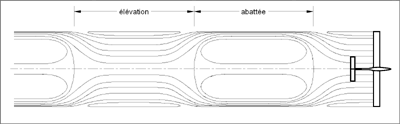
- Système tourbillonnaire derrière
un ornithoptère
dans de conditions d'écoulement quasistationnaires
Le thème de l'ornithoptère touche aussi au domaine de la bionique. On cherche certes à découvrir des ornithoptères capables de voler par la compréhension des principes biologiques concernant la conformation des ailes.
Le Handbuch a été traduit en Français par Jean-Louis Solignac. Avec ses connaissances et son expérience en tant qu'aérodynamicien, il a bien contribué à l'amélioration du Handbuch.
Jean-Louis Solignac, Maître de Recherche, était Chef de Division
Adjoint Aérodynamique Fondamentale
de la Direction Aérodynamique
de l'O.N.E.R.A. (Office National d'Etudes et de Recherches Aérospatiales).
La version française et les photos qui se rapportent au sujet peuvent
trouver place ci-dessous.
- PDF 2.8 Mo
- PDF 6.0 Mo
- PDF 8.9 Mo
Les photographies tirées du Handbuch
2. Calcul de l'aile battante
dans l'hypothèse de conditions quasistationnaires
Les équations tirées du Handbuch sont utilisées dans les différents programmes de calcul Orni- Le schéma suivant est à la base du calcul. Le schéma suivant est à la base du calcul.
L'aile est d'abord divisée en très petites tranches d'envergure. On calcule ensuite pour chacune de ces tranches les forces aérodynamiques dans les conditions d'écoulement stationnaire, c'est-à-dire permanent. On en prend la somme par intégration numérique sur toute l'envergure.
-
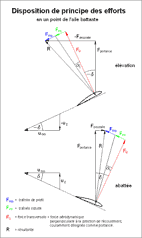
- Disposition des forces
en un point de l'aile battante
De cette façon, on obtient la valeur totale de la portance et de la traînée à un instant donné de la période de battement. On détermine aussi au cours de ce calcul la torsion adéquate de l'aile ainsi que la traînée de profil et la traînée induite.
-
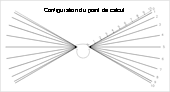
- Configuration du point de calcul
Ce procédé de calcul est répété à des intervalles de temps égaux du mouvement de l'aile. On fixe alors les valeurs susceptibles de changer des facteurs tels que la répartition de la circulation, les conditions de l'écoulement et le configuration du dièdre de l'aile. On suppose en même temps les conditions stationnaires. On suppose donc que l'écoulement ne change pas au cours d'un pas de temps du calcul. Les conditions instationnaires ne sont pas prises en considération.
De cette façon - donc avec pa succession de situations différentes stationnaires - on a une évolution des forces au cours du temps dans des conditions quasistationnaires.
On obtient la force développée sur un mouvement complet par intégration numérique sur les intervalles de temps considérés. On traite au besoin séparément l'élévation et l'abattée de l'aile. En définitive, la somme des efforts développés au cours des battements en élévation et en abattée conduit à l'effort final obtenu sur une période complète.
-
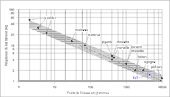
- Fréquence de battement
d'aile et poids de l'oiseau
 Heinrich Hertel 1963
Heinrich Hertel 1963
D'après ![]() Erich von Holst, la méthode quasistationnaire
ne donne de résultat utilisable que dans le cas du vol rapide avec une
faible fréquence de battement (gros oiseaux). Autrement, l'influence des
effets instationnaires est trop forte. De nouvelles publications confirment ces
restrictions, comme par exemple l'analyse suivante de M. Neef.
Erich von Holst, la méthode quasistationnaire
ne donne de résultat utilisable que dans le cas du vol rapide avec une
faible fréquence de battement (gros oiseaux). Autrement, l'influence des
effets instationnaires est trop forte. De nouvelles publications confirment ces
restrictions, comme par exemple l'analyse suivante de M. Neef.
-

- Revised principle arrangement of forces on the flapping wing
In the manual I tried to describe the physical parameters of a flapping wing for a calculation model. In the Arrangement of forces at flapping wing (in German, PDF 0.5 MB) some of them have been redefined.
3. Résultats de la recherche
Dr-Ing. Mathias F. Neef a étudié l'écoulement instationnaire pour une aile en mouvement dans son rapport « Analyse de l'aile battante par un calcul numérique de l'écoulement ». Il parvenait ainsi à un système tourbillonnaire tel que le représente la prochaine figure. Sa représentation avec une allure sinusoïdale du mouvement est plus précise et plus détaillée.
-
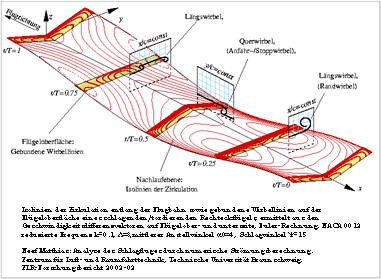
- Lignes d'égale circulation le long de la
trajectoire de vol
dans des conditions d'écoulement non stationnaire
Le rapport contient une vue générale du vol battu et des figures du plus haut intérêt (voir le lien Web 1 et 2).
4. Le tourbillon marginal de l'aile battante
Les « lignes d'égale circulation » représentées ci-dessus peuvent être considérées comme des filets tourbillonnaires.
Des filets tourbillonnaires disposés parallèlement avec une même direction de circulation s'organisent en un tourbillon unique en leur center commun dans le sillage de l'aile.
-

- Tourbillon marginal de l'aile battante
De cette façon, la plus grande partie des filets tourbillonnaires d'un côté de l'aile forment ensemble le tourbillon marginal de l'aile. Leur point d'attache au bord de fuite de l'aile se déplace latéralement au cours d'une période de battement - surtout au cours de l'élévation. Le tourbillon marginal qui subsiste derrière l'aile fait donc voir des contractions latérales régulières.
-
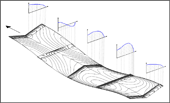
- Reconstitution de la
répartition de la portance
One can derive the lift distributions at the wing from such a vortex image. The position of the vortex filaments at the trailing edge of the flapping wing is used for this purpose. Each vortex filament corresponds to a stage of equal lift size. The closer the vertebral lines are to each other, the greater the change in lift in the concerned wing section. For more information on the procedure, please see Arrangements of wing tip vortices on flapping wings, version 4.2, (PDF 0.5 MB).
In the picture above it is noticeable that the lift distribution in the lower final stroke position is significantly greater than in the upper final stroke position. This is due to the aerodynamic phase shift under non-steady flow conditions. The large lift of the downstroke remains effective over a longer period of time. The same also applies to the upper final stroke position, where the lift is reduced by the previous upstroke. Under stationary flow conditions, the lift distribution of a rectangular wing would be present in both final flapping positions (please look at the dissertation by Dr.-Ing. Matthias F. Neef, e.g. page 204, figue 99, lien Web 1).
Dans le vol de croisière des oiseaux (vol avec la portance
)
le mouvement latéral du tourbillon au bord de fuite de l'aile a déjà
été établi (voir le lien Web 3, Fig.1).
On peut traduire cette caractéristique du vol comme relevant d'une allure
avec un tourbillon continu. Elle présente un contraste avec l'allure d'un
tourbillon annulaire qui est le cas du vol avec la poussée
(voir la description de Le principe du vol).
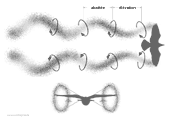
- Tourbillon marginal de l'aile ou
flux propulsif
dans le vol d'un oiseau avec tourbillon continu en vol de croisière
Si on se représente dans l'espace le tourbillon marginal de l'aile sur la figure ci-jointe, on a une image surprenante.
La ligne d'action du tourbillon d'un côté de l'aile ne se contente pas au cours d'une période de battement de se déplacer à droite et à gauche derrière le bord de fuite de l'aile. Elle suit le mouvement de l'aile. Les deux mouvements donnent ensemble, vus dans la direction du vol, une ligne de forme circulaire. Si l'on y rajoute le mouvement d'avancée de l'aile battante, on reconnaît la forme hélicoïdale des deux tourbillons marginaux que l'aile laisse échapper derrière elle.
Les tourbillons marginaux d'une hélice propulsive sont également
organisés sous forme hélicoïdale (voir le lien
Web 4). Ils entourent le flux propulsif dont ils sont partie intégrante.
Par rapport à l'hélice propulsive, la torsion du tourbillon marginal
de l'aile battante s'étire seulement davantage. L'aspect tridimensionnel
de ce tourbillon de chaque côté de l'aile est celui d'un flux
propulsif
.
L'organisation correspondante du tourbillon est aussi à rechercher dans le vol de croisière d'un ornithoptère.Lors de l'élévation une forte portance doit aussi se produire - si possible supérieure à ce qui est présenté ici- et la transition entre les répartitions de la portance entre l'élévation et l'abattée doit être progressive. Dans la séquence filmée du vol d'un cygne, on voit par exemple qu'au cours du battement de l'aile en élévation l'accroissement suivi de la diminution de l'angle d'incidence géométrique de l'aile se déplace comme une onde depuis la racine de l'aile jusque vers son extrémité. For more information, please see the article Arrangements of wing tip vortices on flapping wings, version 4.2, (PDF 0.5 Mo).
5. Le vol en formation des oiseaux
-
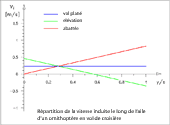
- Répartition de la vitesse induite le long de l'aile d'un ornithoptère en vol de croisière
Dans les formations en vol échelonné en V des oiseaux se présente pour chaque individu une économie de puissance appréciable. Elle provient en particulier d'effets aérodynamiques. A l'aide de la théorie de l'aile battante d'un ornithoptère, on peut tirer des conclusions sur la façon dont se fait cette économie.
En relation avec sa portance, l'oiseau de devant produit nécessairement aux deux extrémités de son aile un tourbillon marginal. Ils signifient pour lui une perte d'énergie. Elle est relativement élevée pour les oiseaux qui ont une forte charge alaire et des ailes courtes et taillées en pointe. L'oiseau qui le suit peut chercher à capter l'énergie de l'un de ces tourbillons pour alléger son propre travail de vol.
-
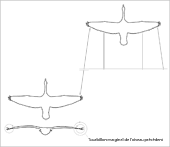
- Réduction de la traînée le vol en formation des oiseaux
On connaît bien l'hypothèse selon laquelle l'oiseau qui suit utilise le champ d'un vent ascendant provenant de celui qui le précède (voir lien Web 5). Ce champ s'étend de l'oiseau vers le tourbillon marginal en arrière du côté extérieur de la formation du vol. Ce vent ascensionnel permet à l'oiseau suiveur d'accroître sa propre poussée sans dépenser lui-même un supplément de travail. Il est toutefois plus efficace pour lui d'utiliser l'impulsion de rotation du tourbillon marginal qui arrive pour réduire son propre tourbillon marginal (voir la figure ci-contre et lien Web 6).
-

- Le vol en formation des oiseaux
Photographe Titus Tscharntke
Le problème de l'oiseau suiveur est de trouver la position optimale parmi
toutes les distances possibles dans l'espace tridimensionnel derrière l'oiseau
qui précède. Il doit rechercher la distance aux ailes battantes
de son prédécesseur de façon à assurer que l'élément
tourbillonnaire adéquat du prédécesseur l'accompagne au moment
opportun et à l'emplacement optimal. Il peut sûrement sentir la meilleure
position, mais doit pourtant aussi faire des compromis. Dans la théorie
du vol en formation des oiseaux, il reste beaucoup de questions ouvertes. Le handbuch
présente la-dessus de plus amples développements (Annexe E).
For more information, please see the article Arrangements
of wing tip vortices on flapping wings, version 4.2, (PDF 0.5 Mo).
6. Liens du Web
sur la théorie de l'aile
battante
- Matthias Neef:
Analyse des Schlagfluges durch numerische Strömungsberechnung
(2002), par exemple page 204, figue 99:
https://publikationsserver.tu-braunschweig.de/receive/dbbs_mods_00001361 - Tatjana Hubel, Untersuchungen zur instationären Aerodynamik
an einem vogelähnlichen Flügelschlagmodell (2006):
http://tuprints.ulb.tu-darmstadt.de/800/ - Tyson L. Hedrick, Bret W. Tobalske and Andrew A. Biewener.
Estimates of circulation and gait change based on a three-dimensional kinematic analysis of flight in cockatiels (Nymphicus hollandicus) and ringed turtle-doves (Streptopelia risoria) (2002), Fig. 1.Continuous-vortex gait
:
https://jeb.biologists.org/content/205/10/1389.full - Prof. Dr.-Ing. Ingo Rechenberg stellt Material für seine Bionik-Vorlesungen
zur Verfügung, zum Beispiel PowerPoint-Script 4:
Vom Vogelflügel zur Windturbine BERWIAN, Verstehen und Kopieren eines biologischen Prinzips
(Randwirbel eines Propellers siehe, Folie 23)
https://www.slideserve.com/halee-atkins/ingo-rechenberg - Malte Andersson and Johan Wallander, Kin selection and reciprocity in flight
formation? :
https://academic.oup.com/beheco/article/15/1/158/331110 - NASA's autonomous formation flight: Follow the leader and save fuel (2001):
https://www.nasa.gov/centers/dryden/history/pastprojects/AFF/index.html















